Tip 1: Hoe de omtrek van een cirkel te vinden, wetende de straal
Tip 1: Hoe de omtrek van een cirkel te vinden, wetende de straal
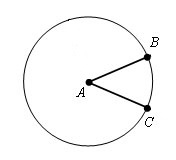
Een cirkel is een gesloten curve in een vlak waarin alle punten even ver verwijderd zijn van een enkel centrum cirkel. onder radius cirkel wordt begrepen als een segment dat het centrum verenigt cirkel met elk punt van een gegeven gesloten curve. Slechts één straal kennen cirkel, je kunt het gemakkelijk vinden lengte.
Je hebt nodig
- De waarde van de straal van een cirkel, de diameter, de waarde van de constante π.
instructie
1
Eerst moet u de brongegevens voor de taak analyseren. Het is een feit dat de conditie ervan niet expliciet kan worden vermeld, wat is de lengte van de straal cirkel. In plaats daarvan kan aan het probleem de lengte van de diameter worden gegeven cirkel. diameter cirkel - een segment dat de twee tegenovergestelde punten combineert cirkel, passerend door zijn centrum. Analyse van de definities cirkel en diameter, kunnen we zeggen dat de lengte van de diameter gelijk is aan tweemaal de lengte van de straal.
2
Nu kun je de straal nemen cirkel gelijk aan R. Dan, om de lengte te vinden cirkel het is noodzakelijk om de formule te gebruiken: L = 2πR = πD, waarbij L de lengte is cirkel, D is de diameter cirkel, wat altijd 2 keer de straal is.
3
Men kan een voorbeeld van de toepassing van deze formule. Gegeven cirkel met een diameter van 8 cm te zien is vereist om te vinden lengte cirkelResolutie: L = 2 * 3.14 * 4 = 3.14 * 8 = 25.12 cm Antwoord: lengte cirkel met een diameter van 8 cm is gelijk aan 25.12 cm
Tip 2: Hoe de diameter van een cirkel uit de lengte te vinden
Cirkel - gesloten curve, alle puntendie zich op gelijke afstand van één punt bevinden. Dit punt is het middelpunt van de cirkel en het segment tussen het punt op de kromme en zijn middelpunt wordt de straal van de cirkel genoemd.

instructie
1
Als we een rechte lijn door het midden van een cirkel trekkenlijn, dan is het segment tussen twee snijpunten van deze lijn met de cirkel de diameter van de gegeven cirkel. De helft van de diameter, van het centrum tot het snijpunt van de diameter met de cirkel, is de straal van de straal. Als de cirkel op een willekeurig punt wordt gesneden, rechtgetrokken en gemeten, is de resulterende waarde de lengte van de gegeven cirkel.
2
Teken verschillende cirkels met een andere oplossingkompas. Een visuele vergelijking stelt ons in staat te concluderen dat een grotere diameter een grotere cirkel begrenst die wordt begrensd door een cirkel met een langere lengte. Bijgevolg is er een direct proportioneel verband tussen de diameter van de cirkel en de lengte ervan.
3
In termen van fysieke betekenis, de parameter "omtrek"komt overeen met de omtrek van een veelhoek die wordt begrensd door een onderbroken lijn. Als we een normale n-gon met kant b in de cirkel opnemen, dan is de omtrek van een dergelijke figuur P gelijk aan het product van zijde b met het aantal zijden van n: P = b * n. De zijde b kan worden gedefinieerd door de formule: b = 2R * Sin (π / n), waarbij R de straal is van de cirkel waarin het n-gon is gegraveerd.
4
Naarmate het aantal zijden toeneemt, wordt de omtrek van het ingeschrevenveelhoek zal benaderen de omtrekslengte L P = b * n = 2n * R * sin (π / n) = n * D * sin (π / n). De relatie tussen de omtrekslengte L en de diameter D constant is. De verhouding L / D = n * sin (π / n) als het aantal zijden van de veelhoek ingeschreven oneindig neigt het getal π, een constante waarde, de "pi" uitgedrukt eindeloze decimale breuk. Voor berekening zonder berekening aangenomen waarde π = 3,14. De lengte van een cirkel en zijn diameter is overgeleverd door de formule: L = πD. De omtrekslengte van de diameter te berekenen delen door het aantal π = 3,14.







