Tip 1: Hoe te bewijzen dat een driehoek een rechthoekig is
Tip 1: Hoe te bewijzen dat een driehoek een rechthoekig is
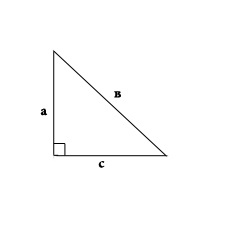
Onder de vele verschillende vormen op het vlak zijn veelhoeken. Het woord "polygoon" geeft zelf aan dat er andere hoeken in deze figuur zijn. driehoek is een geometrische figuur begrensd door drie elkaar kruisende lijnen die drie interne hoeken vormen.
instructie
1
Er zijn verschillende driehoeken, bijvoorbeeld: een hoek van minder dan 90 graden, een rechthoekige driehoek (een hoek van een dergelijke driehoek is precies 90 graden). Overweeg een rechthoekige driehoek en zijn eigenschappen, die worden vastgesteld met behulp van de stelling over de som van de hoeken van een driehoek. Stelling: de som van twee scherpe hoeken van een rechthoekige driehoek is 90 graden. De som van alle hoeken in de driehoek is 180 graden en de rechte hoek is altijd 90 graden. Daarom is de som van de twee scherpe hoeken van een rechthoekige driehoek 90 graden.
2
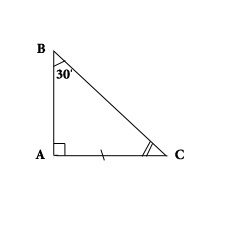
De tweede stelling: de katheter van een rechthoekige driehoek tegenover de hoek van 30 graden is gelijk aan de helft van de hypotenusa. Overweeg de driehoek ABC. De hoek A is recht, de hoek B is 30 graden, vandaar de hoek C is 60 graden. Het is noodzakelijk om te bewijzen dat AC gelijk is aan één seconde voor Christus. Het is noodzakelijk om de driehoek ABD toe te passen op de driehoek ABC. Er wordt een BHD-driehoek verkregen, waarin de hoek B gelijk is aan de hoek D, vandaar dat deze gelijk is aan 60 graden, dus de DS is BC. Maar AC is gelijk aan één seconde DS. Hieruit volgt dat AC gelijk is aan één seconde voor Christus.

3
Als de cathete van een rechthoekige driehoek gelijk is aande helft van de schuine zijde, dan is de hoek die tegen dit been ligt 30 graden - dit is de derde stelling. Het is noodzakelijk om de driehoek ABC te beschouwen, waarin de AU-lus gelijk is aan de helft van de zon (hypotenusa). Laten we bewijzen dat de hoek van ABC 30 graden is. Bevestig de driehoek ABD aan de driehoek ABC. Moet een gelijkzijdige driehoek van VSD zijn (ВС = СД = ДВ). De hoeken van zo'n driehoek zijn gelijk aan elkaar, dus elke hoek is 60 graden. In het bijzonder is de hoek van de verbrandingsmotor 60 graden en is de hoek van de verbrandingsmotor gelijk aan twee hoeken van het ABC. Bijgevolg is de hoek van het ABC 30 graden. Zoals vereist om te bewijzen.

Tip 2: Hoe te bewijzen dat driehoeken gelijk zijn
Twee driehoeken zijn gelijk als alle elementen hetzelfde zijnzijn gelijk aan de elementen van de ander. Maar het is niet nodig om alle dimensies van de driehoeken te kennen om te concluderen dat ze gelijk zijn. Het is voldoende om bepaalde sets parameters van gegeven cijfers te hebben.

instructie
1
Als bekend is dat twee kanten van hetzelfdedriehoeken zijn gelijk aan de twee zijden van de andere en de hoeken tussen deze zijden zijn gelijk, daarna zijn de betreffende driehoeken gelijk. Combineer voor het bewijs de hoekpunten met gelijke hoeken van twee cijfers. Ga door met de overlay. Vanaf het punt dat overeenkomt met twee driehoeken, wijst u de ene kant van de hoek van de bovenliggende driehoek langs de overeenkomstige zijde van de onderste afbeelding. Volgens afspraak zijn deze zijden in twee driehoeken gelijk. Vandaar dat de uiteinden van de segmenten samenvallen. Dientengevolge werd een ander paar hoekpunten in de gegeven driehoeken gecombineerd. De richtingen van de tweede zijden van de hoek van waaruit het bewijs wordt geïnitieerd, vallen samen vanwege de gelijkheid van deze hoeken. En omdat deze zijden gelijk zijn, overlapt de laatste hoek. Tussen twee punten is het mogelijk om een enkele rechte lijn te houden. Dientengevolge vallen de derde partijen in de twee driehoeken samen. Je hebt twee volledig overeenkomende figuren en een bewezen eerste teken van gelijkheid van driehoeken verkregen.
2
Als de zijkant en de aangrenzende twee hoeken in ééndriehoek gelijk zijn aan de overeenkomstige elementen in een andere driehoek, dan zijn deze twee driehoeken gelijk. Om de juistheid van deze verklaring te bewijzen, plaats je twee figuren, waarbij je de hoekpunten van gelijke hoeken combineert met gelijke zijden. Vanwege de gelijkheid van de hoeken zal de richting van de tweede en derde zijden samenvallen en de plaats van hun kruising uniek bepaald zijn, dat wil zeggen dat de derde top van de eerste van de driehoeken noodzakelijkerwijs samenvalt met het analoge punt van de tweede. Het tweede criterium voor de gelijkheid van driehoeken is bewezen.
3
Als drie zijden van een driehoekrespectievelijk gelijk zijn aan drie zijden van de tweede, dan zijn deze driehoeken gelijk. Lijn de twee hoekpunten en de zijkant ertussen uit zodat het ene figuur boven het andere uitsteekt. Plaats de rondbreinaald in een van de gemeenschappelijke hoekpunten, meet de tweede zijde van de onderste driehoek en teken deze straal op de bovenste helft van de compositie van twee driehoeken. Herhaal nu de bewerking vanaf de tweede uitgelijnde hoek met een straal gelijk aan de derde zijde. Maak een inkeping bij de kruising met de eerste boog. Het snijpunt van deze krommen is er slechts één en deze valt samen met de derde top van de bovenste driehoek. Je hebt de bewering bewezen, die in de meetkunde het derde teken van gelijkheid van driehoeken wordt genoemd.







