Tip 1: Hoe de som van een vector te vinden
Tip 1: Hoe de som van een vector te vinden
Vectoren spelen een grote rol in de natuurkunde, omdat ze de krachten op de lichamen duidelijk weergeven. Om problemen in de mechanica op te lossen, moet je, naast kennis van het onderwerp, een idee hebben van vectoren.
Je hebt nodig
- liniaal, potlood.
instructie
1
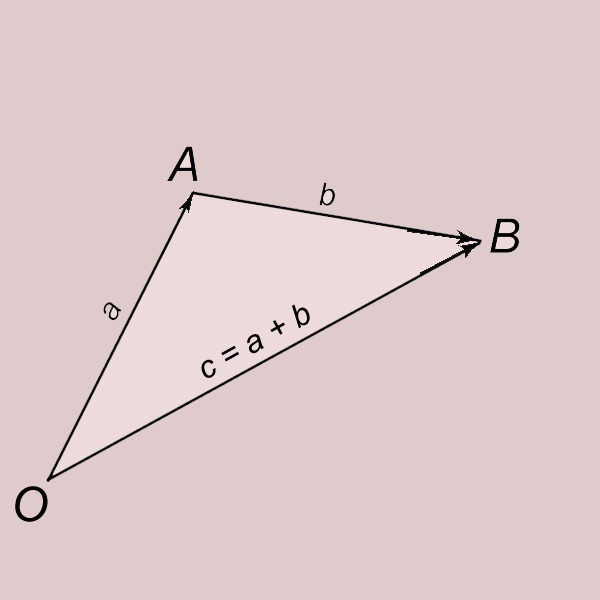
Vectoren toevoegen volgens de regel van een driehoek. Laat a en b twee niet-nulvectoren zijn. We stellen de vector a uit vanaf het punt 0 en duiden het einde aan met de letter A. OA = a. We stellen de vector b uit van punt A en geven het einde aan met de letter B. AB = b. Een vector met oorsprong op punt O en einde op punt B (OB = c) wordt de som van a en b genoemd en schrijf c = a + b. Van de vector c wordt gezegd dat hij wordt verkregen door de vectoren a en b toe te voegen.
2
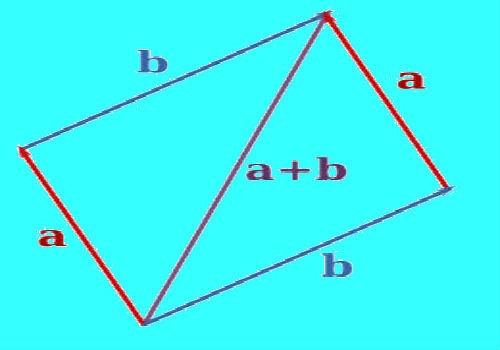
De som van twee niet-collineaire vectoren a en b kan zijnTe construeren door een regel genaamd de parallellogramregel. We stellen uit van het punt A de vectoren AB = b en AD = a. Trek aan het einde van de vector een lijn evenwijdig aan de vector b en door het einde van de vector b een rechte lijn evenwijdig aan de vector a. Laat C het snijpunt van de geconstrueerde lijnen zijn. De vector AC = c is de som van de vectoren a en b. c = a + b.

3
De vector tegenover de vector a wordt genoemdvector, aangeduid - en zodanig dat de som van de vector a en de vektor s gelijk is aan nul vector een + (-a) = 0Vektor tegengestelde vector AV, ook aangeduid BA: BA + AB = AA = 0Nenulevye tegengestelde vectoren gelijke lengten ( | a | = | -a |) en in tegengestelde richtingen.
4
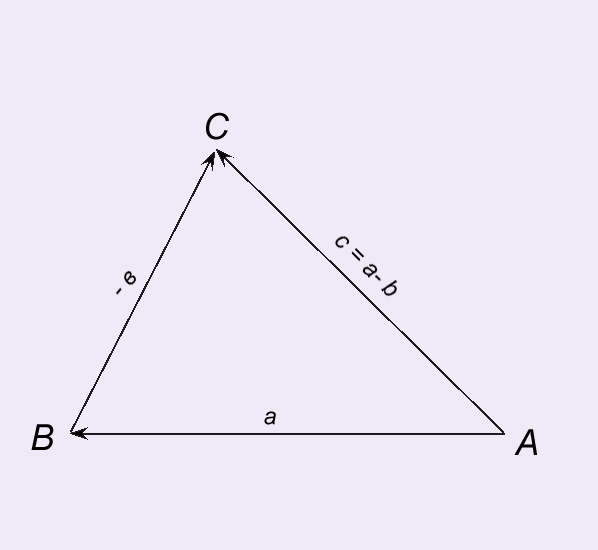
De som van de vector a en de tegenovergestelde vectorde vector b is het verschil tussen twee vectoren a - b, dat wil zeggen de vector a + (-b). Het verschil tussen de twee vectoren a en b is a-b. Het verschil tussen de twee vectoren a en b kan worden verkregen met behulp van de driehoeksregel. We stellen de vector a uit van punt A. AB = a. Vanaf het einde van de vector AB stellen we de vector BC = -b uit, de vector AC = c is het verschil tussen de vectoren a en b.c = a - b.
5
De kenmerken van de werking, toevoeging vectoren: 1) de nulvector eigenschap: a + 0 = a2) associativiteit van toevoeging: (a + b) + c = a + (b + c), 3) commutativiteit: a + b = b + a;
Tip 2: Hoe de som van de coördinaten te vinden
Elk materieel object neemt zijn plaats in de ruimte in. De coördinaten van een fysiek lichaam zijn de numerieke kenmerken van de plaatsing ervan, die de onderlinge positie van objecten bepalen.

instructie
1
Geef het aantal coördinaten op van welke objectenhet is noodzakelijk om het aantal coördinaten te vinden. Een object kan een punt zijn dat langs een coördinaatas beweegt. Het kan nodig zijn om de coördinaten van punten in een vlak of in de ruimte samen te vatten.
2
Als de punten alleen langs een rechte lijn bewegen, hebben dergelijke punten slechts één coördinaat. Lijn de numerieke as uit met de lijn waarop de objecten in kwestie bewegen.
3
Nu is het probleem van het vinden van de som van de coördinaten van twee ofverschillende punten worden teruggebracht tot de bewerking van het toevoegen van positieve en negatieve getallen. Het fundamentele punt is om de nul van het monster te bepalen en aan te geven welke richting vanaf nul als positief wordt beschouwd en die negatief is.
4
Het punt in het vlak wordt gegeven door twee parameters. Om de som van de coördinaten van een punt in een vlak te vinden, voegt u twee getallen toe: de coördinaten van het punt langs de OX-as en langs de OY-as.
5
Bij het bepalen van de som van de coördinaten van een vectorXOY-vlak, zoek eerst de coördinaten van het begin en het einde van de vector. Haal de waarde X van het begin van de vector af van de waarde X van het einde van de vector. Het resulterende getal is de abscis van de vector. Het verschil tussen de waarde van het Y-uiteinde en het begin van de vector is de ordinaat van de vector. Vouw de abscis en de ordinaat van de vector en verkrijg de som van de coördinaten van de vector.
6
Om de som van de coördinaten van het snijpunt te vindentwee rechte lijnen of bochten, moet u eerst deze punten vinden. Het probleem is om een systeem van vergelijkingen op te lossen waarin kruisende lijnen (krommen) worden beschreven. De gemeenschappelijke wortels van de vergelijkingen zijn de gezochte punten van terughoudendheid.
7
Bij het beschouwen van een punt in de ruimte wordt de som van de coördinaten bepaald door drie getallen toe te voegen - de grootheden OX, OY en OZ.