Tip 1: Hoe kan je de hellingshoek bepalen
Tip 1: Hoe kan je de hellingshoek bepalen
hoek huif Elke regel of elk oppervlak kan worden gevonden door de trigonometrische functies te kennen. Ongeacht of je de hoek moet berekenen huif dak, rug van de bank, een paal of een rechte lijn op een vel papier, de methoden voor het bepalen van de hoek hetzelfde zijn.

Je hebt nodig
- - Roulette;
- - een loodgieterij;
- - technische rekenmachine.
instructie
1
Om de hoek te weten te komen huif, construeer een rechthoekige driehoek, hellendDe lijn zal werken als een hypotenusa. Gebruik hiervoor een schietlood, omdat deze altijd een rechte hoek maakt met de grond. Selecteer het startpunt op uw hellend vlak of lijn en meet de afstand van dit punt tot de grond (of een ander horizontaal oppervlak, zoals de vloer) met een schietlood en meetlint. Als er geen loodlijn is, neem dan gewoon de lading en hang het aan het touw. Deze afstand wordt het tegenovergestelde been genoemd.
2
Meet vervolgens de afstand vanaf het punt waaroprustte uw loodlijn, tot het punt waarop het hellende oppervlak tegen de grond (vloer) rust. Dit is de aangrenzende kathet. Als deze afstand moeilijk te vinden is, vervangt u deze met de lengte van het hellende oppervlak van het beginpunt naar de grond (vloer). Het zal een hypotenusa zijn. Hoe dan ook, tot uw beschikking moeten ten minste twee cijfers zijn - de hypotenusa en een van de benen, of twee benen.
3
Als u de lengte van de hypotenusa en de lengte kenttegenover het been, tel de sinus (sin), waarbij de lengte van het been wordt gedeeld door de lengte van de hypotenusa. Om de hoek zelf te vinden, gebruik je de engineeringcalculator om de arcsine (arcsin) van het verkregen getal te vinden. Let op, in de rekenmachine kan de aanduiding zijn: sin ^ (- 1) of asin. Je krijgt de waarde van de hoek in graden.
4
Als je de lengte van het aangrenzende been weet enhypotenusa, vind de cosinus (cos), hiervoor, verdelen de lengte van het been in de lengte van de schuine zijde. Neem de calculator met de arcos (of acos, of cos ^ -1) en tel de arccosinus, die de gewenste hoek is huif in graden.
5
Om de hoek te meten huif met bekende benen, vind de tangens (tg). Om dit te doen, verdeel de tegenovergestelde tangens in de aangrenzende tangens. Bereken vervolgens vanaf dit getal met de rekenmachine arctg (het kan ook worden aangeduid met atan of tan ^ -1). De verkregen waarde is de hoek in graden.
Tip 2: Hoe de kantelhoeken van een vlak te bepalen
Bij de productie van diverse werken in de dacha of(plotten van verschillende plaatsen, plaveiselplaten of paden) moeten vaak worden gekoppeld aan hellende paden van de site, op verschillende niveaus. Het is nodig om de hellingshoeken van het vliegtuig op zulke gebieden zorgvuldig te bepalen en te onderhouden.

Je hebt nodig
- - verticaal of horizontaal bouwniveau;
- - een loodgieterij;
- - goniometer;
- - Protractor;
- - platte houten staaflengte van 1,5 m;
- - laserniveau en meetregelaar;
- - hydro level, marker, 2 pegs;
- - Roulette.
instructie
1
Om de hellingshoek van het vliegtuig te bepalenGebruik op de eenvoudigste manier een loodgieter, houten staaf en gradenpoot. Plaats de balken op het testvlak. Houd de linkerhand vast met de loodlijn op een hoogte van 300 - 400 mm. Trek de loodlijn naar de rand van de balk. Kalmeer de bodem van de loodlijn. Plaats met je rechterhand de verticaal plat op de staaf. Bewegingsgraad, combineer het vertrekpunt van de graden met de loodlijn. Overweeg de hellingshoek van het vliegtuig bij het kruispunt van de loodlijn met de schaal van de lengteboog. Verkrijg een hellingshoek van het vliegtuig met betrekking tot de verticale. Als u een hoek ten opzichte van de horizon nodig heeft, bereken dan door af te trekken van de resulterende hoek 90. Gebruik deze methode voor het afronden van metingen, omdat het een lage nauwkeurigheid geeft bij het meten van de hoek van het vlak.
2
De volgende meetmethode is nauwkeuriger. Plaats de balken op het testvlak. Zet het niveau verticaal aan de rand van de balk. Houd het niveau met uw linkerhand. Bevestig met de rechterhand de lengteboog naar de resulterende randen van de hoek. Overweeg op de schaal van de gradeboog de waarde van de hellingshoek van het vliegtuig.
3
De meest nauwkeurige manier waarop toegepast islaser niveau. Stel de basis van het niveau horizontaal in. Zet de laserkop aan. Meet het niveau van het hoogteverschil van de horizontale laserstraal naar het oppervlak van het geteste vlak in een lengte van 1 m. Bij een druppel van maximaal 1 m in deze sectie is elke 2.22 cm van de druppel bijna 1 graad.
4
Een hoge nauwkeurigheid van het meten van de hellingshoek kanbereiken, gebruikmakend van het hydroniveau in plaats van het laserniveau. Voor deze meting, hamer twee pinnen op een afstand van 1 m parallel aan de helling van het vlak.Markeer de horizon met een hydraulisch niveau op hen. Meet de afstand van de horizonlabels tot het vlak. Neem een kleiner formaat van een groter formaat - verkrijg de waarde van het hoogteverschil op een afstand van een meter. Scheid deze waarde met 2,22 en verkrijg de hellingshoek van het gemeten deel van het vlak in graden.
Tip 3: Hoe de afstand in Google te meten
Hoe te achterhalen de afstand tussen punt A en punt B op een Google-kaart? Een pijnlijk bekende vraag, toch? Met de cartografische service van Google is het vrij eenvoudig om te bepalen de afstand naar een weinig bekende stad aan de andere kant van de wereld of hoe ver van je huis de dichtstbijzijnde halte is.
Je hebt nodig
- Internet toegang
instructie
1
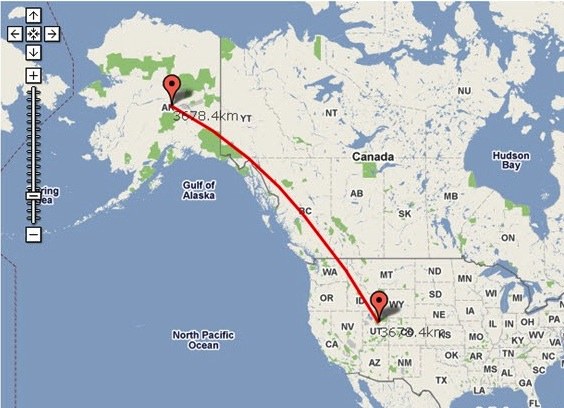
Ga naar de Google-zoekmachine en klik op het woord"Kaarten", die is gelegen op de top van poiskovika.S rechterkant zult u de kaart zien, en aan de linkerkant zijn twee knoppen: "Routes" en de "My Places". Klik op "Routes". Daaronder ziet u twee van het venster "A" en "B", dat wil zeggen de begin- en eindpunten otscheta.Dopustim, bent u in Ufa, en je moet weten hoe lang het de weg naar Perm zal nemen. In dit geval wordt het venster "A" schrijven "Ufa" en in de "B" - "Perm". Nogmaals, klikt u op de knop onder de vensters "Routes" .Op de kaart zal volgen, en onder de ramen van de "A" en "B", hoeveel kilometers van de ene stad naar de andere, maar ook hoeveel tijd je nodig hebt om te besteden aan de mashine.Esli neemt u geïnteresseerd bent in wandelen zijn loop, klik op de knop met de afbeelding van de voetganger, die zich boven de vensters "A" en "B" bevindt. De service zal de route opnieuw opbouwen en automatisch berekenen de afstand en de verwachte tijd onderweg.
2
In het geval dat het nodig is om te meten de afstand van punt "A" naar "B", gelegen in éénDe schikking moet worden uitgevoerd volgens het hierboven beschreven schema. Het enige verschil is dat je met de naam van het gebied een straat en eventueel een huisnummer moet toevoegen via een komma. (Bijvoorbeeld "A": Moskou, Tverskaya 5 en "B": Moskou, Tsvetnoy Boulevard, 3).
3
Er zijn situaties waarin u geïnteresseerd bent de afstand tussen objecten "direct": door velden, bossen en rivieren. Klik in dit geval op het pictogram met de getande ring in de bovenhoek van de pagina. Selecteer in het uitgevouwen menu dat verschijnt, "Google Maps Lab" en schakel het gereedschap voor afstandsmeting in, sla de wijzigingen op. De liniaal verscheen in de linkerbenedenhoek van de kaart, klik erop. Markeer het referentiepunt op de kaart en vervolgens het eindpunt. Tussen deze punten verschijnt een rode lijn op de kaart en verschijnt er een afstand op het paneel aan de linkerkant.
Tip 4: Hoe de tangens van de tangenshoek te vinden
De geometrische betekenis van de eerste orde afgeleidefunctie F (x) is de raaklijn naar de grafiek, die door een bepaald punt van de curve loopt en op dit punt ermee samenvalt. En de waarde van het derivaat op een gegeven punt x0 is de helling of anderszins - de tangens van de hellingshoek van de raaklijn k = tan a = F '(x0). De berekening van deze coëfficiënt is een van de meest voorkomende problemen in de theorie van functies.

instructie
1
Noteer de gegeven functie F (x), bijvoorbeeld F (x) =(X³ + 15 x 26). Als het probleem duidelijk wordt aangegeven via welke een raaklijn, zoals de coördinaten x0 = -2, kan worden afgezien plotten functies en aanvullende lijnen op het cartesiaanse systeem OHY. Vindt de eerste orde afgeleide van de voorafbepaalde functie F` (x). In dit voorbeeld F` (x) = (3x² + 15). Vervangen door een vooraf bepaalde waarde van het argument x0 de afgeleide van de functie en de waarde te berekenen: F` (-2) = (3 (-2) ² + 15) = 27. Aldus, je vond tg a = 27.
2
Bij het overwegen van een taak waar deze moet worden bepaaldde tangens van de hellingshoek van de tangens op de grafiek van de functie op het snijpunt van deze grafiek met de abscisas, moet u eerst de numerieke waarde van de coördinaten van het snijpunt van de functie met OX vinden. Voor de duidelijkheid, is het het beste om een grafiek van een functie op een tweedimensionaal OXY-vlak te construeren.
3
Specificeer een coördinatenreeks voor abscissen, bijvoorbeeld-5 tot 5 stappen 1. Substitutie van de waarde x, berekening van het relevante functie in de ordinaat en die op het referentievlak verkregen door het punt (x, y). Verbind punten met een vloeiende lijn. U ziet op de uitvoering van de dienstregeling kruising van de functie van de x-as. De ordinaat van de functie op dat moment nul is. Vind de numerieke waarde van het overeenkomstige argument aan haar. Hiertoe een voorafbepaalde functie, zoals F (x) = (4x² - 16) wordt op nul gezet. Los het resulterende vergelijking met een variabele x en bereken: 4x² - 16 = 0, x² = 4, x = 2. Aldus, afhankelijk van de toestand van het probleem, de helling van de raaklijn aan de grafiek van de functie moet een punt met de coördinaten x0 = 2 zijn.
4
Vergelijk net als bij de eerder beschreven methodede afgeleide van de functie: F` (x) = 8 * x. Bereken vervolgens de waarde ervan op het punt met x0 = 2, wat overeenkomt met het snijpunt van de oorspronkelijke functie met OX. Vervang deze waarde in de afgeleide van de functie en bereken de tangens van de raaklijnhoek: tg a = F` (2) = 16.
5
Wanneer u de hoekcoëfficiënt op het snijpunt van de functiegrafiek met de ordinaatas (OY) vindt, voert u de vergelijkbare bewerkingen uit. Alleen de coördinaat van het gewenste punt x0 moet onmiddellijk gelijk aan nul worden genomen.







