Tip 1: Een boom van problemen opbouwen
Tip 1: Een boom van problemen opbouwen
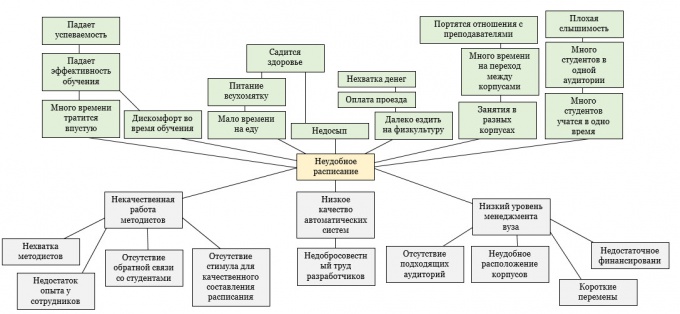
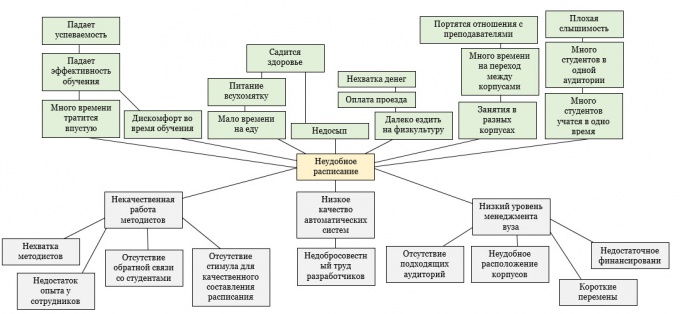
De probleemboom is een sleutelhet proces van vorming van taken in de onderneming en het zoeken naar oplossingen vergemakkelijken. Hiermee kan het hele spectrum van onderling samenhangende oorzaken en gevolgen van het probleem worden bepaald, waarbij de invloed van externe subjectieve factoren vrijwel volledig wordt uitgesloten. De probleemstructuur is een van de belangrijkste hulpmiddelen bij systeemanalyse. Laten we de constructie van dit model beschouwen aan de hand van het voorbeeld van een lastig tijdschema in een universiteit.
instructie
1
Formuleer het probleem. Het moet in het heden bestaan, niet in het verleden of in de toekomst. Formuleer specifiek, vermijd onnodige woorden. Probeer de mondiale problemen aan te pakken, die praktisch onmogelijk te beïnvloeden zijn ("broeikaseffect", "zielloosheid van de samenleving", enz.).

2
Maak een lijst met belanghebbenden. Dat wil zeggen, het is noodzakelijk om alle deelnemers te identificeren die direct of indirect door dit probleem worden beïnvloed. Hiervoor moet je de volgende vragen beantwoorden. Op wie heeft dit probleem de grootste impact? Wie neemt er direct deel aan de oplossing van het probleem? Welke organisaties of groepen mensen kunnen de loop van het werk beïnvloeden? Bepaal precies hoe een geïnteresseerde persoon afhankelijk is van het probleem.

3
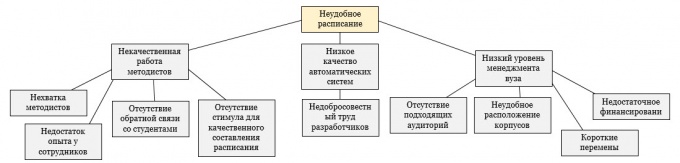
Begin met het bouwen van een boom van problemen. Het bestaat uit drie delen: wortels, stam en kroon. Wortels zijn de oorzaken van het probleem. Zij bepalen zelf het bestaan ervan. Als je ze oplost, verdwijnt het probleem. De stam is de formulering. Crohn - dit zijn de gevolgen die het probleem veroorzaakten. Teken eerst een vat.

4
Vervolgens moet je de wortels tekenen. Noteer eerst alle redenen die in uw brainstormsessie naar voren komen. Groepeer ze en geef de relaties aan. Probeer het maximale aantal "roots" te vinden, omdat het hun beslissing is die een beslissende invloed zal hebben.
5
Het laatste punt is de kroon. Identificeer de onmiddellijke contactpunten tussen het probleem en de gevolgen. Houd vervolgens bij wat andere negatieve gevolgen kunnen hebben, dat wil zeggen naar het niveau hieronder gaan. Blijf dit doen zolang de gevolgen nog steeds deel uitmaken van het probleem.
Tip 2: Hoe een root in een grafiek te bouwen
Elke functie, inclusief een kwadratische functie, kan in een grafiek worden geconstrueerd. Om dit grafische beeld te construeren, worden de wortels van de gegeven kwadratische vergelijking berekend.

Je hebt nodig
- heerser;
- - een simpele potlood;
- - een notitieboekje;
- - de handgreep;
- - sjabloon.
instructie
1
Zoek de wortels van de kwadratische vergelijking. Een kwadratische vergelijking met een onbekende is als volgt: ax2 + bx + c = 0. Hier is x het onbekende; a, b en c zijn bekende coëfficiënten, en a mag niet 0 zijn. Als u beide zijden van de gegeven kwadratische vergelijking deelt met a, krijgt u een gereduceerde kwadratische vergelijking van de vorm x2 + px + q = 0, waarin p = b / a en q = c / a. Op voorwaarde dat een van de coëfficiënten b of c, of beide gelijk is aan nul, wordt de kwadratische vergelijking die u hebt verkregen onvolledig genoemd.
2
Zoek de discriminant die wordt berekend doorformule: b2-4ac. In het geval dat de waarde van D groter is dan 0, heeft de kwadratische vergelijking twee echte wortels; als D = 0, zullen de gevonden echte wortels aan elkaar gelijk zijn; als D
3
Grafische weergave van een kwadratische functiezal een parabool zijn. Definieer aanvullende gegevens voor het plotten van de grafiek van deze kwadratische functie: de richting van de "takken" van de parabool, de vertex en de vergelijking van de symmetrieas. Als a> 0, dan zijn de "takken" van de parabool naar boven gericht (anders worden de "takken" naar beneden gericht).
4
Om de coördinaten van de vertex van de parabool te bepalen, zoek je x met de formule: -b / 2a, en dan vervang je de waarde van "x" in de kwadratische vergelijking om de waarde van y te verkrijgen.
5
Ten slotte is de vergelijking van de symmetrie-as afhankelijk vande waarden van de coëfficiënt c in de oorspronkelijke kwadratische vergelijking. Als de gegeven kwadratische vergelijking y = x2-6x + 3 bijvoorbeeld is, dan zal de symmetrieas langs de lijn gaan waarin x = 3.
6
Wetende de richting van de "takken" van de parabool, de coördinaten van zijnhoekpunten, evenals de as van symmetrie, construeren een grafiek van een gegeven kwadratische vergelijking met behulp van een sjabloon. Label de wortels van de vergelijking op de afgebeelde afbeelding: het zijn de nullen van de functie.







